Available Animations
Shannon-Fano Compression
The Shannon-Fano compression algorithm first examines all elements of the text (or binary data) to be compressed and counts their frequency in the source. It then sorts the actual symbols contained in the source by descending frequency, so that the most common element will be at the left and the least common one at the right. It then segments the list into two sections such that the sum of the number of occurrences of elements to the left is as close to the sum of occurrences of the elements to the right as possible. A 0 is then assigned to the left section, and a 1 to the right section, and the algorithm recursively continues splitting and assigning a value until no further split is possible. In this way, each input element will be assigned a sequence of 0/1 values - and thus a binary encoding. The source data is then compressed by replacing each element of the source with its binary encoding, which will typically have a far shorter length (at least, for the more common elements) than the usual 8 bit encoding.
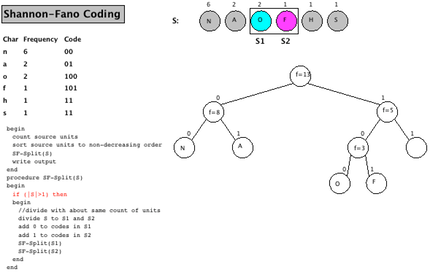
In the generator, the user can specify a string to be encoded; the default string to be encoded is "shannonfannon", where it is obvious that "n" is the most common character (6 occurrences), followed by "a" and "o" with two occurrences each, and the other characters ("s", "h", "f") with one occurrence each.
The algorithm starts with a verbal description of the algorithm, as shown below.

In the next step, the process of segmenting the elements into two halves and assigning a bit value, and the further segmenting elements. At the time of the screenshot, "N", "A", "O" and "F" have already been assigned a final code, and the process has to continue for "H" and "S".
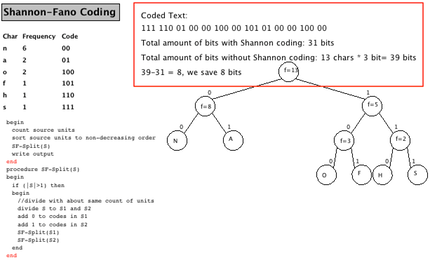
The animation ends with the final encoding for each input character, as shown in the table to the left in column "Code", and also visible in the tree. It also provides the Shannon-Fano encoding of the source and gives a rough approximation of the space saved (highlighted here with a red box which is not part of the actual animation).
Example Animation: LZW Compression
In this example posting, we examining one concrete output of the generation process. Because this is the first such step, we will provide a few more details than we will do in later postings.
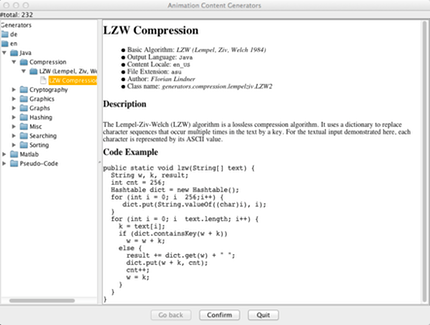
First, start the generation process as outlined in the blog posting How to create a new animation using a generator by selecting File ➜ Generate…. Then navigate to English (en), Java, Compression, and choose the algorithm LZW (Lempel, Ziv, Welch). You will see a window as blow that gives some basic details on the generator, includings its author and the name of the class (in case something was broken, you can use this to report a precise error). You can also see the underlying implementation code in Java at the bottom.
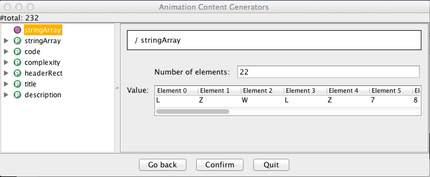
Next, click on Confirm to see the options. The algorithm has one parameter, as also indicated on the screenshot above, called stringArray in this case. You can adjust the value by modifying the length of the array ("Number of elements" - please make sure to press RETURN when you change the size to notify the Java program of the change!). Here, we leave the array in its default state, which was chosen to give some helpful output.
We could also modify the display options of six different entries, but we will leave them alone here. Click Confirm to confirm the values, and then either choose a filename to save the file (and load it in later), or click Confirm again to directly see the animation.
The animation starts with a very brief overview of the algorithm and how it works "in plain English". There is no screenshot for this here; put simply, the algorithm maintains a dictionary of entries, where each "word" is associated with a number. The dictionary initially contains the entries 0-255 for the 256 entries in the ASCII character set. Whenever a new word combination is encountered, for example "LZ", the algorithm checks if this "word" is already in its dictionary. If this is the case, we add the next input character and repeat the process. If not, the new "word" is added to the dictionary at the next free position and the encoding for the "last known word" (shorter by the last character) is added to the encoded output.
In the next image, you see the main animation. The red code line is the one currently being executed, in the context of the "else" statement. We have just added the text LZ77 to our dictionary with the numerical value 262. The last output was 259, representing the LZ7 part of the "word" that was already contained in the dictionary. The next word to be encoded would be 7L, using the last 7 of the previously unknown word LZ77 and the next character (right next to the arrow) L; this will again be added to the dictionary as a new element and the code for 7 (55) will be added to the output.

One of the great advantages of the LZW compression algorithm is that the dictionary can be rebuilt from the compressed contents and thus does not have to be transferred, saving network bandwidth and/or disk space.
Why don't you try out the generator on your own?
Overview of the different algorithm topic categories
The following algorithm topic categories are currently supported and filled with at least some content in the ANIMAL AV system. Please note that some of the categories may only provide examples for a certain combination of natural and programming language!
- Backtracking algorithms try out one possible solution for a problem until they have either solved the problem or found a "dead end". In the latter case, they go backwards one step ("backtrack") and take the next possible route - again, until the problem has been solved or a "dead end" has been encountered. A "dead end" is typically an illegal state, the meaning of which depends on the underlying problem. For example, in the "8 Queens Problem", eight queens have be placed on a chessboard so that no queen may strike another queen. Here, an illegal state occurs whenever one queen can strike another one (note: this will always be due to the last queen placed). In other applications, a state may be "illegal" if its result is already worse than the best result found so far.
- Compression algorithms describe how content can be stored using less space than if it were stored directly - and of course how the original content can be restored from the "space-shrunk version". Typical and popular examples include space-saving storage of images (for example, using the JPG or PNG format instead of the bitmap-based BMP format), audio (MP3 versus WAV), video (MP4 and other formats), as well as the compression of large archives (ZIP being probably the most well-known format) - which are also typically used when you download Windows, Linux, or Mac OS X installation files.
- Cryptography algorithms deal with making content "unreadable", or at least harder to read, for unintended parties - and how to restore the actual content by the intended recipient. As such, they are widely used in communication, for example in the https:// protocol that indicates an encrypted data transmission between your browser and the server, and should be used whenever privileged data such as passwords or bank account-related information is transferred.
ANIMAL is - together with its cryptographic visualisations for Caesar, Vigenere, Nihilist and DES - part of the wide-spread, open-source e-learning program CrypTool v1 (http://www.cryptool.org). - Data structures algorithms portray the characteristic behaviour of a given data structure, for example how data is inserted, found, or deleted.
- Graph algorithms include many algorithms in Computer Science that deal for example with finding the cheapest route from one node to another. They are used in many concrete problems, so that a good understanding of graph algorithms is very important for a good programmer.
- Graphics algorithms deal with approaches to render objects on the screen, or determine which objects shall be shown in which order and to what degree. For example, if a 5000x3000 pixels large image shall be shown on a far smaller area, it either has to be scaled "appropriately" to fit the area available to it, or it should be "cropped": those portions of the image not visualizable on the output area do not have to be drawn, saving computation effort.
- Hardware-based algorithms visualize the behaviour of the hardware components underlying modern computers, for example logic gates or multiplexers.
- Hashing algorithms allow the representation of arbitrary content linked to a "key". For example, the complete data of a student may be retrieving by providing the student's student ID as the "key". If used properly, hashing allows "instanteous" access, avoiding the effort to search for the data in a collection, such as a list or array.
- Mathematics also contains a set of algorithms, although mathematicians would typically not label them in that way. This includes various approaches to determine eigenvalues, invert matrices, or (cleverly) multiply matrices.
- Misc is the "catch-all" category for all algorithms that do not fall into any of the other categories.
- Networking algorithms portray Internet protocols and their data flow or show how the (typically graph-based) routing algorithms that determine how to send data from client A to client B work.
- Searching algorithms deal with finding a given element in a collection. Apart from well-known algorithms such as Binary Searching, this also includes other applications, such as finding a text inside a larger text - a typical application for any text editor (but harder to implement well than one might at first think!).
- Sorting algorithms work on reordering a collection of elements into a well-defined order. The order can be rather straightforward (e.g., ascending numbers), but can also be more elaborate (e.g., phone books order persons by family name, followed by first name, street and then phone number if the previous entries were identical).
- Tree algorithms work on another very important data structure used in many algorithms. They can be used for easy and efficient navigation among elements, and to represent hierarchical structures, among (many) other applications.
As you can see, there is a lot to explore using ANIMAL!
How to create a new animation using a generator
In this step-by-step guide, you will see how easy it is to create a new animation using one of the many content generators provided by ANIMAL.
Go to the main menu of ANIMAL, open the File menu and then select the entry Generate…
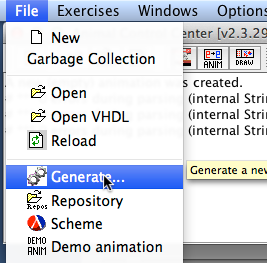
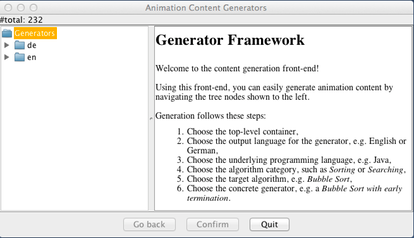
After a short moment, the window for the Animation Content Generators will open:
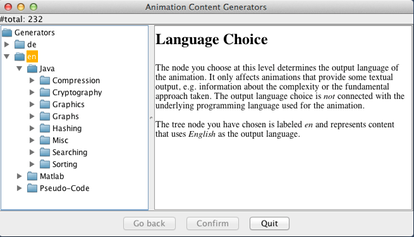
First, select the target language. This determines in what language the textual comments - not the program itself - will be shown, if any. Here we have selected en for English. Please also note how the program explains each step as you click on an entry in the unfolding tree.
In the next step, you can choose the programming language of the underlying implementation. Typically, you will be able to choose at least between Java and Pseudo Code, a textual description of what the algorithm does. Since this step is not very surprising in its content, we do not offer an image for this step.
Now choose the concrete algorithm category. The prepared categories include the most common applications for undergraduate CS students and programmers, such as compression, cryptography, graphics, graphs, hashing, searching, sorting, maths and miscellaneous. Again, the category will described in the panel to the right.
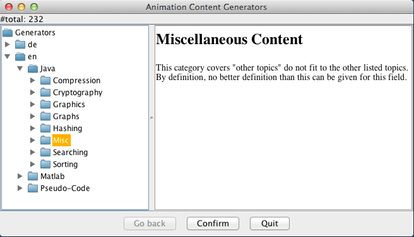
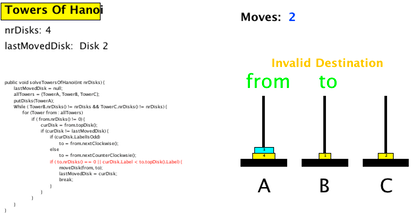
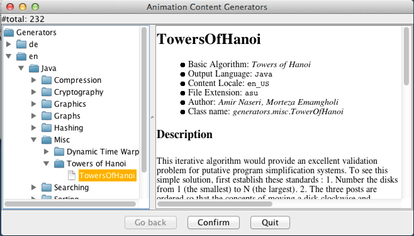
Once you have opened the category, you will see a list of concrete algorithms available in the category. Here, we select the Towers of Hanoi algorithm. Note how the panel on the right will display author information, a description of the algorithm, and below an overview of the underlying code. This information shall help you in figuring out if this was exactly what you were looking for.
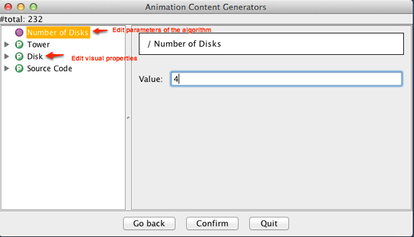
After confirming that this is indeed what you were looking for, you will be taken to a view where you can modify both the parameters of the algorithm (indicated by a purple circle before their name) and/or visual properties of the animation. In this example, there is only one parameter ("Number of Disks", which we have changed from its default value 3 to 4), and three different visual properties you can adjust, defining how a tower, disk and the source code shall be displayed. When you are done, press Confirm.
Now you can choose whether you want to save the animation (click on Browse… for this purpose and choose a directory and filename), or want to directly see the result (simply click on Confirm without choosing a filename first).
Finally, here is the animation content. Note that you will also be asked if you want to close the generator window or not (not shown here).